Z-Score

[eSignal]

File Name: Z_Score.efs

Description:
Z-Score

Formula Parameters:
Period : 20

Notes:
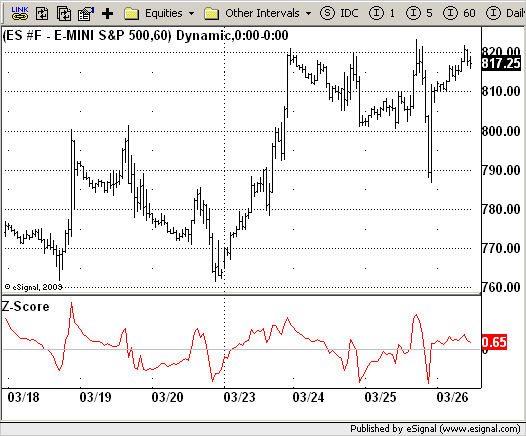
The author of this indicator is Veronique Valcu. The z-score (z) for a data
item x measures the distance (in standard deviations StdDev) and direction
of the item from its mean (U):
z = (x-StdDev) / U
A value of zero indicates that the data item x is equal to the mean U, while
positive or negative values show that the data item is above (x>U) or below
(x Values of +2 and -2 show that the data item is two standard deviations
above or below the chosen mean, respectively, and over 95.5% of all data
items are contained within these two horizontal references (see Figure 1).
We substitute x with the closing price C, the mean U with simple moving
average (SMA) of n periods (n), and StdDev with the standard deviation of
closing prices for n periods, the above formula becomes:
Z_score = (C - SMA(n)) / StdDev(C,n)
The z-score indicator is not new, but its use can be seen as a supplement to
Bollinger bands. It offers a simple way to assess the position of the price
vis-a-vis its resistance and support levels expressed by the Bollinger Bands.
In addition, crossings of z-score averages may signal the start or the end of
a tradable trend. Traders may take a step further and look for stronger signals
by identifying common crossing points of z-score, its average, and average of average.


Download File:
Z_Score.efs



EFS Code:

/*********************************
Provided By:  
    eSignal (Copyright c eSignal), a division of Interactive Data 
    Corporation. 2009. All rights reserved. This sample eSignal 
    Formula Script (EFS) is for educational purposes only and may be 
    modified and saved under a new file name.  eSignal is not responsible
    for the functionality once modified.  eSignal reserves the right 
    to modify and overwrite this EFS file with each new release.

Description:        
    Z-Score

Version:            1.0  03/24/2009

Formula Parameters:                     Default:
    Period                              20

Notes:
    The author of this indicator is Veronique Valcu. The z-score (z) for a data 
    item x measures the distance (in standard deviations StdDev) and direction 
    of the item from its mean (U):
        z = (x-StdDev) / U
    A value of zero indicates that the data item x is equal to the mean U, while 
    positive or negative values show that the data item is above (x>U) or below 
    (x Values of +2 and -2 show that the data item is two standard deviations 
    above or below the chosen mean, respectively, and over 95.5% of all data 
    items are contained within these two horizontal references (see Figure 1).
    We substitute x with the closing price C, the mean U with simple moving 
    average (SMA) of n periods (n), and StdDev with the standard deviation of 
    closing prices for n periods, the above formula becomes:
        Z_score = (C - SMA(n)) / StdDev(C,n)
    The z-score indicator is not new, but its use can be seen as a supplement to 
    Bollinger bands. It offers a simple way to assess the position of the price 
    vis-a-vis its resistance and support levels expressed by the Bollinger Bands. 
    In addition, crossings of z-score averages may signal the start or the end of 
    a tradable trend. Traders may take a step further and look for stronger signals 
    by identifying common crossing points of z-score, its average, and average of average. 
**********************************/

var fpArray = new Array();
var bInit = false;

function preMain() {
    setStudyTitle("Z-Score");
    setCursorLabelName("Z-Score", 0);
    setDefaultBarFgColor(Color.red, 0);
    addBand(0, PS_SOLID, 1, Color.lightgrey);
    
    var x=0;
    fpArray[x] = new FunctionParameter("Period", FunctionParameter.NUMBER);
    with(fpArray[x++]){
        setLowerLimit(1);        
        setDefault(20);
    }
}

var xZ_Score = null;

function main(Period) {
var nBarState = getBarState();
var nZ_Score = 0;

    if (nBarState == BARSTATE_ALLBARS) {
        if(Period == null) Period = 20;
    }    
    if (bInit == false) {
        xZ_Score = efsInternal("Calc_Z_Score", Period, sma(Period), close());
        bInit = true;
    }
    
    nZ_Score = xZ_Score.getValue(0);
    if (nZ_Score == null) return;
    return nZ_Score;
}

function Calc_Z_Score(Period, xMA, xClose) {
var nRes = 0;
var StdDev = 0;
var SumSqr = 0;
var counter = 0;
    if(xMA.getValue(0) == null) return;
    for(counter = 0; counter < Period; counter++)
        SumSqr += Math.pow((xClose.getValue(-counter) - xMA.getValue(0)), 2);
    
    StdDev = Math.sqrt(SumSqr / Period);
    
    nRes = (xClose.getValue(0) -  xMA.getValue(0)) / StdDev;    
    return nRes;
}